Paper Summary: A Particle Batch Smoother Approach to Snow Water Equivalent Estimation
Published:
Today I want to write about a paper from a couple years ago coauthored by a colleague of mine, Dr. Gonzalo Cortés. I have worked with Gonzalo through the California Data Collaborative, and I might end up working with him in the future if the funding works out, so I have started working my way through a literature review of papers that will be relevant for the project.
The paper for today is Margulis et al. (2015) A Particle Batch Smoother Approach to Snow Water Equivalent Estimation. I want to begin by saying that I have ZERO background in hydrology and earth sciences, so this probably the first academic hydrology paper that I have ever read. Fortunately this is a methods paper with a data assimilation algorithm at its core, so I was reasonably in my element while reading. The whole concept of data assimilation has apparently been around for decades in earth science circles, but this was my first exposure to the technique as an urban/data scientist. I must say the approach is really quite general and I have already thought of some cool applications in the urban domain (maybe I’ll write about this in the future).
Before I get too far off topic, I will get on to the contents of the paper and hopefully not butcher it too much. Please be advised that any errors are certainly my own failure to grasp the content and not indicative of the authors’ work.
How to accurately estimate the amount of water stored in mountain snowpack?
The primary goal of this paper is to lay out a very accurate method for estimating Snow Water Equivalent (SWE) which is the hydrology term-of-art for the volume of water stored in snow. Specifically, Margulis et al. want to know about SWE stored in mountains because mountain snowpack is the primary water source for more than 1/6 (!!) of the world population and also because it is a more challenging estimation problem because of the complexities of mountain topography.
The main components of this method are
A land surface model (LSM), also called the “forward model” that takes meteorological and topographical variables as input (e.g. wind, precipitation, solar radiation, slope, elevation, etc.) and then models physical processes to predict the amount of snow present in each grid cell of the simulation at a given time.
A Snow Depletion Curve (SDC) model, aka the “measurement model” that takes SWE as an input and predicts the fractional Snow Covered Area (fSCA), which is the proportion of land area that is covered by snow.
An update step that takes the prior estimates of SWE from the LSM and conditions them on satellite measurements of fSCA so that the posterior model estimates more closely match the observations.
This update framework itself is not novel to the paper, but rather the core contribution of this paper is to use a Particle Batch Smoother (PBS) approach to conduct the update. It turns out that the PBS approach delivers radically improved estimates of SWE when compared to a previously proposed approach based on a Kalman filter.
Graphical representation
I was struck by the similarities of this method to another topic I have been studying recently: bayesian networks. I am sure that there are some sort of deep mathematical connections here that would be obvious if I ever manage to get past the first few chapters of Gelman’s Bayesian Data Analysis book, but for the time being I am operating mainly at an intuitive level.
The diagram below is my own and shows my understanding of the relationship between the different variables.
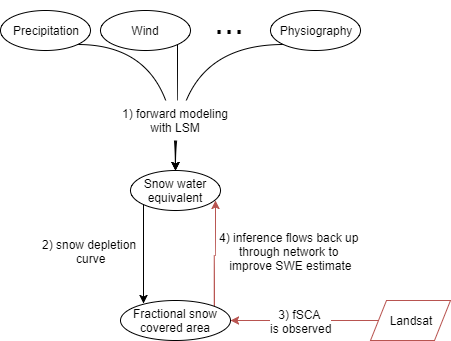
If we consider how influence flows through a conditional probability network like this, then we can see that by observing the “bottom” node representing fSCA, we can propagate that knowledge up the graph for insight into the middle state representing SWE.
Simplified summary
The authors embed their approach in a very legitimate probabilistic framework, but I always try to understand mathematical concepts using my intuition rather than relying just on formulas. So I will try to summarize the approach intuitively.
First, take a bunch of meteorological variables and make them stochastic by multiplying them by an assumed prior distribution. Then take a Monte Carlo approach by sampling from these input distributions to create big vectors of possible input realizations.
Then feed each realization of the joint input distribution through an Simplified Simple Biosphere Model (a.k.a. a really complicated LSM) to obtain a prior distribution of SWE.
Pass this prior distribution of SWE through the measurement model to obtain a prior joint distribution of SWE and fSCA. Without getting too mathy, let’s call this prior Y+.
Use PBS to assign a weight to each replicate/realization/particle in Y+ by calculating the difference between the prior fSCA for that replicate and the OBSERVED fSCA measured using Landsat images. Each weight is derived by plugging the error term (prior - observation) into a Gaussian with mean 0 and variance derived (I think) from the overall error distribution.
These weights then effectively give us our desired posterior distribution of SWE.
How good is it?
The authors spend the rest of the paper validating their approach and comparing its performance to a prior approach. Suffice to say that the method works REALLY WELL.
Takeaways
I was really excited by the paper. Probably because I am methods nerd at heart and I love seeing cool applications of data analysis techniques applied to solve scientific problems. I also enjoy diving into an entirely new field like this and poking around, trying to guage the extents and gaps of my knowledge.
